Parallel computing and GPU programming with Julia

Part I: Multi-threading

Alexis Montoison

using Base.Threads
using BenchmarkTools

• Thread is the smallest unit of executable code that performs a particular task.
• Threads are execution units within a process that can run simultaneously. While processes are separate, threads run in a shared memory space (heap).
• An application can divided into multiple tasks and each can be assigned to a thread.
• Many threads executing simultaneously is termed as multi-threading.

In Julia, all relevant functions for multi-threading are in the Threads library. How many threads do we have access to?

Threads.nthreads()

we will need more than one thread to be able to gain any performance from multi-threading...

Julia can be started with a given number of threads in different ways:

JULIA_NUM_THREADS=4 julia  # we can also set the `JULIA_NUM_THREADS` environment variable in .bashrc.
julia -t 4
julia --threads 4
julia -t auto

The main multithreading approach is to use the Threads.@threads macro which parallelizes a for loop to run with multiple threads. Let us operate on the array a simultaneously using 4 threads. We'll have each thread write its thread ID into each location.

Note: 4 is the number of threads on my computer.

a = zeros(Int, 10)
Threads.@threads for i = 1:10
    a[i] = Threads.threadid()
end
display(a)

The iteration space is split among the threads. What is the difference between :static and :dynamic schedulers?

function busywait(seconds)
    tstart = time_ns()
    while (time_ns() - tstart) / 1e9 < seconds
    end
end

@time begin
    Threads.@spawn busywait(5)
    Threads.@threads :static for i in 1:Threads.nthreads()
        busywait(1)
    end
end

@time begin
    Threads.@spawn busywait(5)
    Threads.@threads :dynamic for i in 1:Threads.nthreads()
        busywait(1)
    end
end

function sqrt_array(A)
    B = similar(A)
    for i in eachindex(A)
        @inbounds B[i] = sqrt(A[i])
    end
    B
end

function threaded_sqrt_array(A)
    B = similar(A)
    @threads for i in eachindex(A)
        @inbounds B[i] = sqrt(A[i])
    end
    B
end

n = 1000
A = rand(n, n)
@btime sqrt_array(A);
@btime threaded_sqrt_array(A);

Do we have the correct result?

sqrt_array(A) ≈ threaded_sqrt_array(A)

With 4 threads, the speedup could be about a factor of 3

function sqrt_sum(A)
    s = zero(eltype(A))
    for i in eachindex(A)
        @inbounds s += sqrt(A[i])
    end
    return s
end

function threaded_sqrt_sum(A)
    s = zero(eltype(A))
    @threads for i in eachindex(A)
        @inbounds s += sqrt(A[i])
    end
    return s
end

n = 1000
A = rand(n, n)
@btime sqrt_sum(A);
@btime threaded_sqrt_sum(A);

sqrt_sum(A) ≈ threaded_sqrt_sum(A)

# Ref{Int} is an object that safely references data of type Int.
# This type is guaranteed to point to valid, Julia-allocated memory of the correct type.
acc = Ref{Int}(0)
@threads for i in 1:1000
    acc[] += 1
end
acc[]

With multi-threading we need to be aware of possible race conditions, i.e. when the order in which threads read from and write to memory can change the result of a computation.

You are entirely responsible for ensuring that your program is data-race free. Be very careful about reading any data if another thread might write to it!

Julia supports accessing and modifying values atomically, that is, in a thread-safe way to avoid race conditions. A value (which must be of a primitive type) can be wrapped as Threads.Atomic to indicate it must be accessed in this way. Here we can see an example:

acc = Atomic{Int}(0)
 @threads for i in 1:1000
    atomic_add!(acc, 1)
end
acc[]

i = Threads.Atomic{Int}(0)
old_i = zeros(4)
Threads.@threads for id in 1:4
    old_i[id] = atomic_add!(i, id) # Threads.atomic_add! returns the old value of i!
end
display(i[])
old_i

Let's solve the race condition in our previous example:

function threaded_sqrt_sum_atomic(A)
    T = eltype(A)
    s = Atomic{T}(zero(T))
    @threads for i in eachindex(A)
        @inbounds atomic_add!(s, sqrt(A[i]))
    end
    return s[]
end

@btime threaded_sqrt_sum_atomic(A);

function threaded_sqrt_sum_optimized(A, partial)
    T = eltype(A)
    @threads for i in eachindex(A)
        @inbounds partial[threadid()] += sqrt(A[i])
    end
    s = zero(T)
    for i in eachindex(partial)
        s += partial[i]
    end
    return s
end

partial = zeros(Float64, nthreads())
A = rand(5000,2000)
@btime sqrt_sum(A);
@btime threaded_sqrt_sum_optimized(A, partial);

We observe that:

• The serial version provides the correct value and reference execution time.
• The race condition version is both slow and wrong.
• The atomic version is correct but extremely slow.
• The optimized version is fast and correct, but required refactoring.

Conclusion: Threads is as easy as decorating for loops with @threads, but data dependencies (race conditions) need to be avoided. It sometimes requires code refactorization. Using atomic operations adds significant overhead and thus only makes sense if each iteration of the loop takes significant time to compute.

Exercise: Multithread the computation of π

Consider the following function which estimates π by “throwing darts”, i.e. randomly sampling (x,y) points in the interval [0.0, 1.0] and checking if they fall within the unit circle.

function estimate_pi(num_points)
    hits = 0
    for _ in 1:num_points
        x, y = rand(), rand()
        if x^2 + y^2 < 1.0
            hits += 1
        end
    end
    fraction = hits / num_points
    return 4 * fraction
end

num_points = 100_000_000
@btime estimate_pi(num_points)  # 3.14147572...

function threaded_estimate_pi_v1(num_points)
    hits = Atomic{Int}(0)
    @threads for _ in 1:num_points
        x, y = rand(), rand()
        if x^2 + y^2 < 1.0
            atomic_add!(hits, 1)
        end
    end
    fraction = hits[] / num_points
    return 4 * fraction
end

num_points = 100_000_000
@btime threaded_estimate_pi_v1(num_points)

function threaded_estimate_pi_v2(num_points)
    partial_hits = zeros(Int, nthreads())
    @threads for _ in 1:num_points
        x, y = rand(), rand()
        if x^2 + y^2 < 1.0
            partial_hits[threadid()] += 1
        end
    end
    hits = sum(partial_hits)
    fraction = hits / num_points
    return 4 * fraction
end

num_points = 100_000_000
@btime threaded_estimate_pi_v2(num_points)

julia -t 1 threaded_estimate_pi.jl
pi = 3.14176872
time = 950.957122

julia -t 2 threaded_estimate_pi.jl
pi = 3.1412234
time = 732.195929

julia -t 4 threaded_estimate_pi.jl
pi = 3.14180932
time = 663.25783

Parallel scaling is not linear with the number of threads! Comparing to the unthreaded version reveals the overhead from creating and managing threads.

Tools for multi-threading

• OhMyThreads.jl: Simple tools for basic multithreading.
• ThreadsX.jl: Parallelized Base functions
• Tullio.jl: Tullio is a very flexible einsum macro (Einstein notation)
• (LoopVectorization.jl): Macro(s) for vectorizing loops.
• (FLoops.jl): Fast sequential, threaded, and distributed for-loops for Julia

Homework 🤓

• Implement a multi-threaded version of the dot product between two vectors.
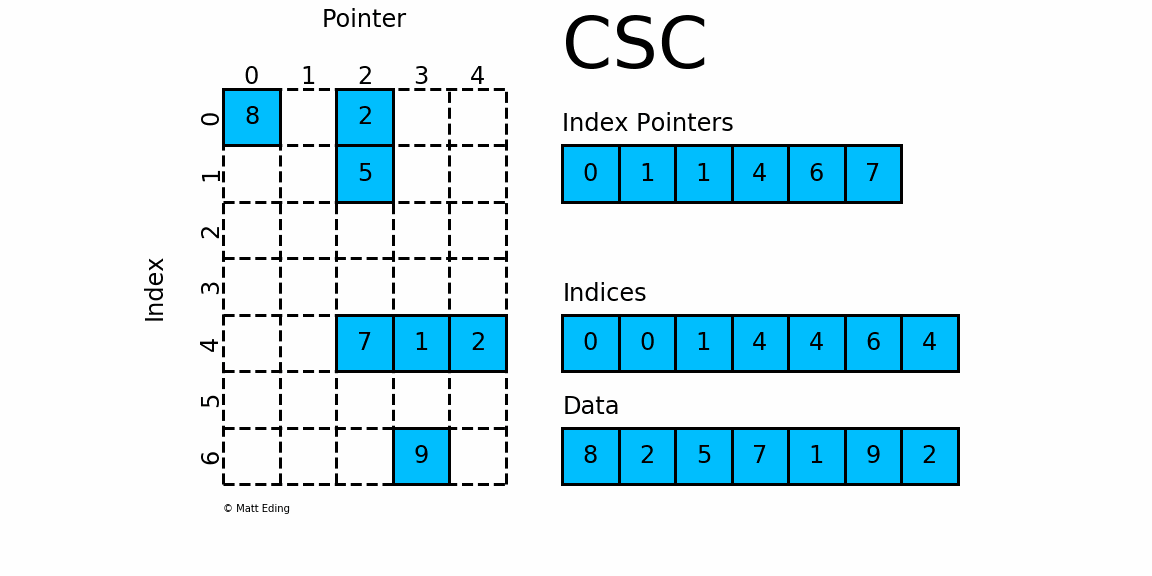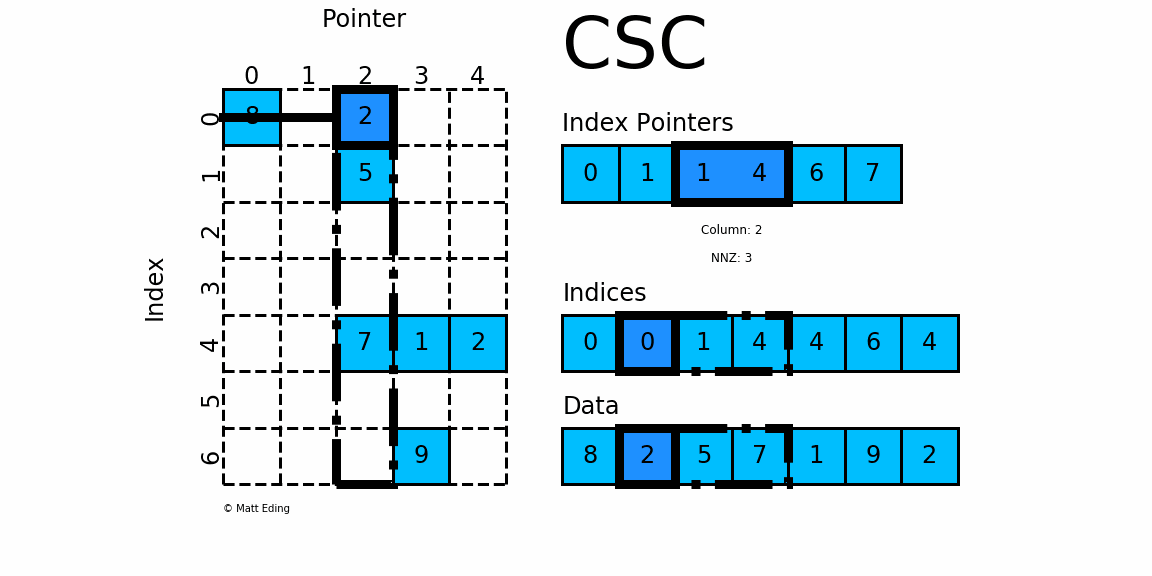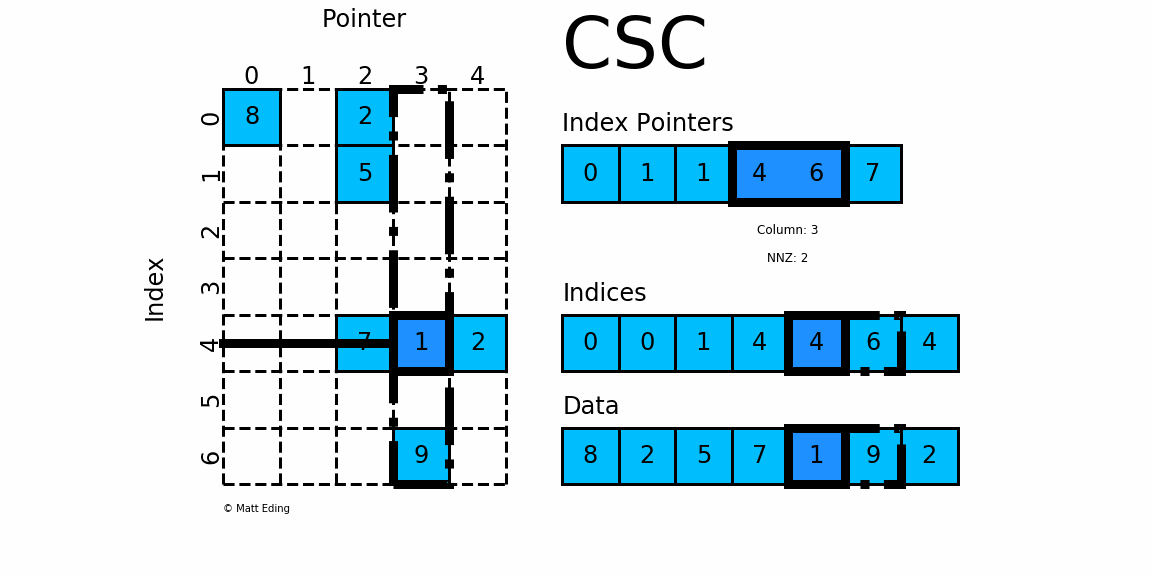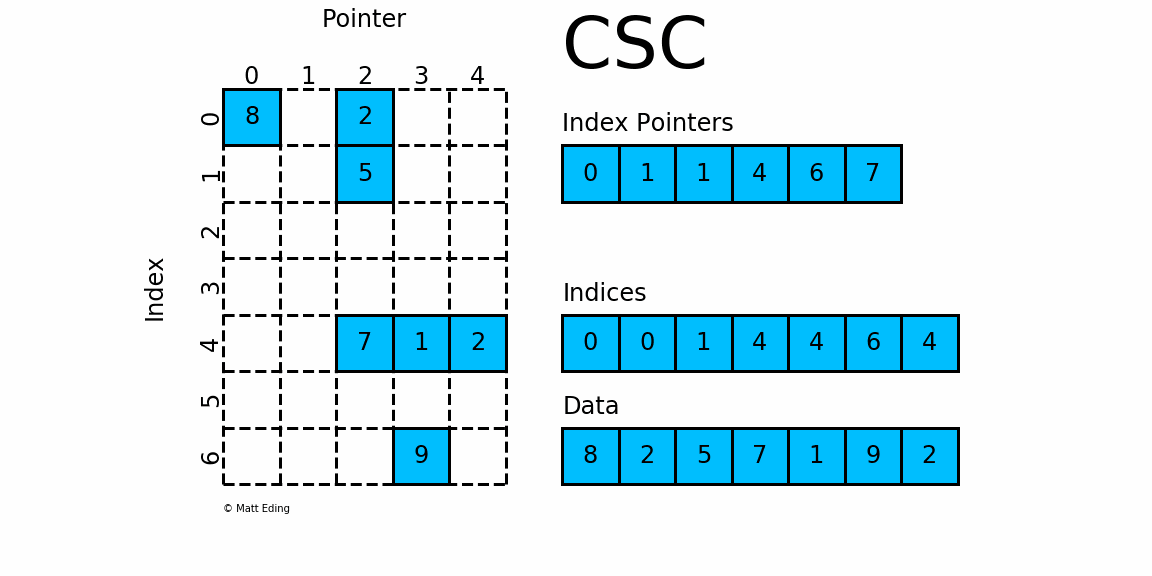
• Implement a multi-threaded version of the matrix-vector products A * v and Aᵀ * v where A is a SparseMatrixCSC. Explain which product is more adapted for multi-threading.

References:

• https://docs.julialang.org/en/v1/base/multi-threading
• https://enccs.github.io/Julia-for-HPC/multithreading
• https://miro.medium.com/v2/resize:fit:4800/format:webp/1*2JKgg1exEuvgO8mLfEEmRg.png